1.1  ค่า SE ของ mean LDL = 18 /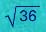  =  3
           ที่ 95 % CI ของ mean LDL = 120 ฑ t.₀₅  SE
           จากตารางค่า t ที่ df 35,     t = 2.03
           95 % ของ mean LDL  = 120 ฑ 2.03(3)
                                             = 120 ฑ 6.09
                                             = 113.91 , 126.09
           นั่นคือ 113.91 < m < 126.09
           เราสามารถเชื่อมั่นได้ 95 % ว่าค่าเฉลี่ยของ LDL โดยทั่วไปจะอยู่ระหว่าง  113.91 ถึง 126.09 mg/dl

    1.2  ค่า SE ของ mean HDL    =  6 /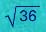  =  1
           95 % CI ของ mean HDL = 41 ฑ 2.03 (1)
                                                 = 38.97,  43.03
           เราสามารถเชื่อมั่นได้ 95 % ว่าค่าเฉลี่ยของ HDL โดยทั่วไปจะอยู่ระหว่าง  38.97 ถึง 43.03  mg/dl

    1.3  ค่า t ที่  90 %CI ,   a = 0.1     df  = 35
           ในตาราง  t = ฑ  1.69   ในทำนองเดียวกันจะได้ว่า
           90 % CI ของ mean LDL = 120 ฑ 1.69 (3)
                                                 = 114.93,  125.07
           นั่นคือ   114.93 < m < 125.07
           90 % CI ของ mean HDL  =  41 ฑ 1.69 (1)
                                                  =  39.31,   42.69
           นั่นคือ   39.31 < m <  42.69
            จะเห็นได้ว่าเมื่อความเชื่อมั่นลดลงมาเป็น 90 % ค่าประมาณที่ได้จะมีช่วงแคบกว่าที่ความเชื่อมั่น 95 % และเมื่อ ความเชื่อมั่นลดลงมา ความคลาดเคลื่อน (a) ก็เพิ่มมากขึ้น